介绍
早期的单片传感器LM3911,LM134和LM135等克服了许多困难,但它们的输出是相关的到开尔文温度标度,而不是更流行的摄氏和华氏度标。幸好,1983年,两个I.C.,LM34精密华氏温度传感器和LM35精密摄氏温度介绍了温度传感器。
LM34的输出为10 mV /°F,在-50至+ 300°F范围内的典型非线性度仅为±0.35°F温度范围,通常在室温(77°F)时精确到±0.4°F之内。
LM34的低电压输出阻抗和线性输出特性使与读数或控制电路的连接变得容易。LM34相对于其他当前可用温度传感器的固有优势在于它不像易受低电平泄漏电流的影响而导致输出错误。例如,许多单片温度传感器的输出仅为1μA/°K。
LM34的低电压输出阻抗和线性输出特性使与读数或控制电路的连接变得容易。LM34相对于其他当前可用温度传感器的固有优势在于它不像易受低电平泄漏电流的影响而导致输出错误。例如,许多单片温度传感器的输出仅为1μA/°K。
仅在1μA的电流下导致1°K的误差漏电流。另一方面,LM34可以用作电流模式设备,提供20μA/°F输出电流。相同的1μA泄漏电流将导致LM34的输出误差仅为0.05°F(或缩放后为0.03°K)。
通过在机床上执行修整和校准程序,可以保持低成本和高精度。晶圆水平。该设备可以使用单电源或双电源供电。小于70μA的LM34具有电流消耗功能,自发热极小(在静止空气中小于0.2°F),并采用TO-46金属制成
LM34的先驱
温度传感器的制造取决于利用某种材料的特性,即温度的变化函数。优选地,该函数将是温度的线性函数兴趣范围。硅NPN晶体管的基极-发射极电压(VBE)具有这样的温度在小温度范围内的依赖性。不幸的是,VBE的值在整个生产范围内变化,因此室温校准未指定或确保生产中没有错误。
另外,温度系数约为−2 mV /°C也具有公差并在生产中扩展。此外,尽管速度可能呈线性在狭窄的温度范围内,在整个-55°C至300°C的范围内,存在高达3°C或4°C的确定非线性。+ 150°C温度范围。
已经开发出另一种方法,其中两个晶体管的基极-发射极电压之差在不同电流密度下工作的温度被用作测量温度。可以看出两个晶体管Q1和Q2以不同的发射极电流密度工作,它们的基极发射极电压之差ΔVBE为
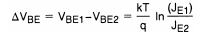
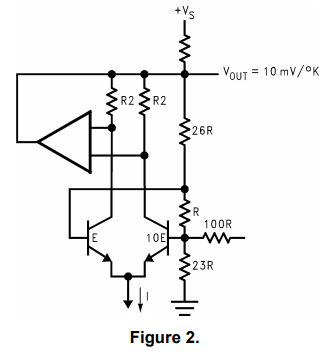
其中k是玻尔兹曼常数,q是电子上的电荷,T是绝对温度,以度为单位开尔文和JE1和JE2分别是Q1和Q2的发射极电流密度。 实现这一点的电路功能如图1所示。
公式1表示只要IE1与IE2之比保持恒定,则ΔVBE是的线性函数。温度(在整个温度范围内并非完全正确,而是用于VBE1和VBE2的非线性将在后面讨论)。该ΔVBE与温度的线性良好足以使当今大多数单片温度传感器都基于此原理。
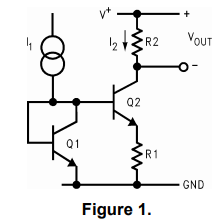
使用上述原理的早期单片温度传感器如图2所示。输出与绝对温度标度相关的电压,每度10 mV开尔文并被称为LM135。该电路的ΔVBE约为:(0.2毫伏/°K)×(T)(2)在电阻R两端产生。放大器用作伺服器以强制这种情况。
出现ΔVBE然后将电阻R两端的电阻乘以由R组成的电阻串以及26R和23R电阻输出电压为(10 mV /°K)×(T)。标有100R的电阻器用于失调微调。这个电路一直很流行,但是这种开尔文温度传感器的缺点是常数大输出电压2.73V,必须减去后才能用作摄氏温度标度传感器。
已经开发出各种传感器,其输出与摄氏温度成比例规模,但价格昂贵,并且由于需要大量的校准步骤而难以校准必须执行。
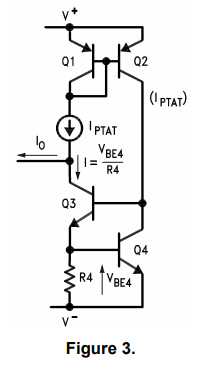
杰拉德·C·M。 Meijer [4]开发了一种电路,该电路声称具有固有的如果在任何一种温度下适当修整,则校准。电路的基本结构如下所示图3.输出电流的温度系数为1μA/°C。该电路的工作原理如下:与绝对温度成比例的电流IPTAT由电流源产生。
然后一个从IPTAT中减去与晶体管Q4的VBE压降成正比的电流以获得输出当前,IO。晶体管Q4通过PNP电流镜和晶体管Q3偏置,该晶体管用作反馈放大器。在论文中,声称校准过程非常简单且可以通过调整电阻器R4调整灵敏度dIO / dT。
然后在任何温度下执行修整PTAT电流源中的电阻以给出正确的输出电流值进行校准的温度。Meijer的摄氏温度传感器由于其输出信号较小而存在问题(也就是说,输出可能有因漏电流引起的错误)。另一个问题是修剪方案需要修剪两个电阻的精度很高。
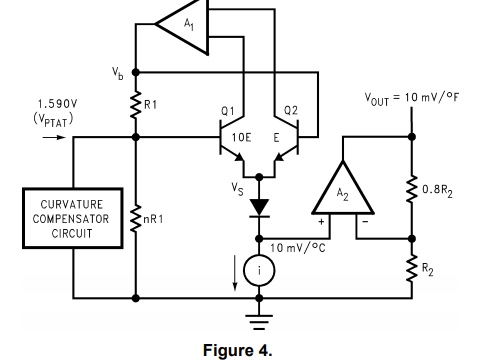
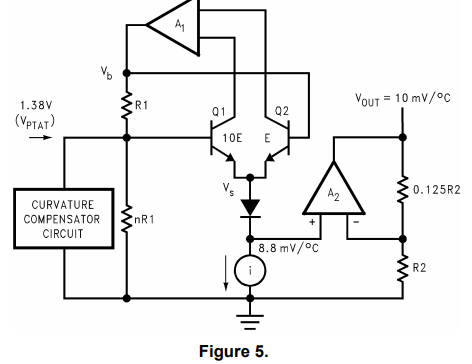
为了克服这些问题,图4中的电路LM34华氏温度传感器)和图5(LM35摄氏温度传感器)已经过开发具有更简单的校准程序,具有相对较大温度系数的输出电压和曲率补偿电路,以解决VBE与温度之间的非线性特性。基本上,发生的事情是晶体管Q1和Q2在电阻R1两端形成一个ΔVBE。
这个电压是在电阻nR1上相乘。因此,在放大器A2的同相输入端是一个电压两个二极管压降低于电阻nR1两端的电压。然后,该电压由放大器A2放大以提供输出与所需的任何温度标度成比例,每度为10 mV
电路操作
由于两个电路非常相似,因此仅在LM34华氏温度传感器中进行讨论。更详细的信息。该电路如下操作。
晶体管Q1具有晶体管Q2发射极面积的10倍,因此,电流密度的十分之一。从图4中可以看出,Q1和Q2的电流密度之差将产生一个电压。与电阻R1两端的绝对温度成正比。在77°F时,该电压将为60 mV。
如开尔文(Kelvin)温度传感器,放大器A1用于通过伺服驱动器来确保这种情况晶体管Q1的基极电压升至ΔVBE×n的电压电平VPTAT。 n的值将在校准设备以在任何温度下提供正确的输出。
出于讨论目的,假设VPTAT等于1.59V的值将给出正确的770输出mV在77°F。那么n将等于VPTAT /ΔVBE或1.59V / 60 mV = 26.5,并且VPTAT将具有一个温度系数为:
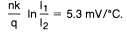
将两个581 mV(在77°F下)的二极管压降分别与-2.35 mV /°C的温度系数相减,将导致放大器A2的同相输入端的电压为428 mV,温度系数为10 mV /°C。如图所示,放大器A2的增益为1.8,可在77°F(25°C)时提供至770 mV的必要转换。
一种再举一个例子,如果温度为32°F(0°C),则A2输入处的电压为428 mV–(10 mV /°C)(25°C)= 0.178,这将使VOUT =(0.178)(1.8)= 320 mV-正确的值在这个温度下
简易校准程序
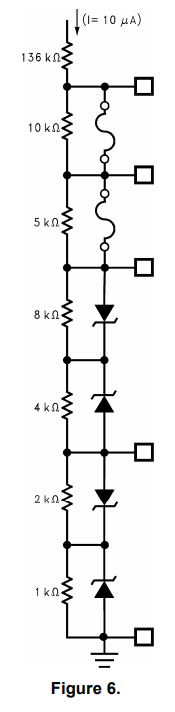
通过调节电阻比系数n的值,可以在任何温度下对电路进行校准。 注意n的值取决于两个二极管的电压降的实际值,因为n为调整以提供正确的输出电压值,而不是PTAT的理论值。该通过打开或短路准二元微调网络的链路,可以轻松执行校准程序,如图6所示。
可以通过炸开铝制保险丝来打开连接以增加阻力,或者通过执行“齐纳击穿”将电阻从电路中短路。 接下来的分析部分显示了在给定温度下校准电路后,电路将是准确的在整个温度范围内。